One of the most significant obstacles, which must be overcome in imaging astronomical objects, is the inherent faintness of these objects. From the early days of photographic film to present day CCDs, great strides have been made in capturing and rendering these faint objects. With the advent of CCD technology an astro-imager was no longer plagued by photographic film reciprocity failure and finally had a linear detector to capture these objects. The most efficient way (in terms of detector speed) at present to capture these faint objects in color is to take three filtered images and combine them into a single color image. The traditional methodology of producing color astronomical images is to take an image through a red, green, and blue filter and combine the three into a color image. This process was first developed in the 19th century and applied to film emulsions to produce the first color photographs.

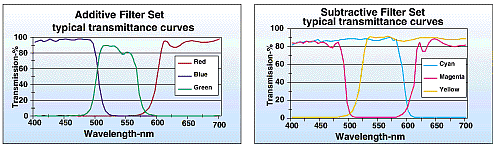
In 1998 Al kelly, Richard Berry, Chuck Shaw and Ed Grafton began to experiment with using cyan, magenta and yellow filters to produce color astronomical images in stead of using the traditional red, green, and blue methodology. Since the cyan magenta and yellow are each comprised of two colors each (and thereby passing twice as much data per unit exposure time), it seemed as if this methodology would be more efficient that the traditional red, green, blue (RGB) methodology. The charts below show the typical band pass of characteristics of RGB and CMY filter sets.

R = M + Y - C

G = C + Y - M

B = C + M - Y

The derivation of the RGBs from CMY data has the effect of degrading the S/N ratio of the RGBs derived from CMY filters. The reason is that noise adds as the root sum of squares so the RGB derivatives adds sqrt(3) to the noise. Since the signal is twice as large the S/N is degraded by a factor of sqrt(2/3). The S/N of an RGB derived from a CMY data set has 81% the S/N ratio of RGBs from RGB filters. So the CMY RGBs are noisier than the RGBs from RGB filters.

In practice many if not most imagers are producing images that are LRGB or WCMY. So what does this mean to the S/N of a LRGB compared to a WCMY image?

Suppose we wanted to bring the CMY RGBs up to the S/N level of the RGBs from RGB filters. Let the R, G and B filter Signal=S, then the C, M and Y filter signal=2S and an IR blocked "L" or "W" image would have a signal of 3S. Let the noise for each image = N.

1) The RGB S/N is = S/sqrt(S)

2) The RGB S/N for CMY derived RGBs is = 2S/(Sqrt(sqrt(2S)^2 + sqrt(2S)^2 + sqrt(2S)^2)) = 2S/Sqrt(6S). If the exposure of the CMYs were increased by 50% then:

3) Then equation 2 becomes 3S/(sqrt(sqrt(3S)^2 + sqrt(3S)^2 + sqrt(3S)^2)) = 3S/sqrt(9S) = S/sqrt(s) = to equation 1

The math shows that you would need 50% longer exposures for the CMYs to get to the same S/N level as the RGBs from RGB filters.

Now lets construct the luminance (W) from these 50% longer CMY images (as I typically do) and compare them to the luminance constructed from the RGB filters and also do the same for the RGBs

4) The W for the 50% longer CMY exposures = 3s+3s+3S/(sqrt(sqrt(3S)^2 + sqrt(3S)^2 + sqrt(3S)^2))= 9S/sqrt(9S)

5) The L for the RGBs is = 3S/sqrt(3S)

6) Dividing eq.4 by equation 5 = 1.73 = 173%

The math shows that the SNR of the constructed W from the CMYs is 173% better than the L constructed from the RGB filters. So with a 50% longer exposure for the CMY you will get 173% better luminance S/N and equal S/N on the chrominance.

Now instead of equalizing the chrominance, lets equalize the luminance by taking longer RGB exposures.

Since the RGB signal = S and CMY signal = 2S:

The math shows that you would need to take 100% longer exposures through the RGBs to construct an L that has the same S/N of the CMY constructed W image, but the RGBs (do some more math) would have a chrominance S/N that is 173% better than the CMY chrominance derived RGBs.

Now lets go back to where we had equal chrominance S/N (this is where we had to have 50% longer CMYs) and a W S/N that was 173% better than the RGBs. In order to bring the LRGB L image up to the S/N of the W (173% better S/N) from the 50% longer CMYs, we will take a no filtered L image and add it to the RGBs to construct a L that has the same S/N as the W. This means that the chrominance and the luminance will then have the same S/N for each method.

7) From equation 4 the W image has a S/N of 9S/sqrt(9S).

8) The L (R+G+B+L) image would have a S/N = S+S+S+3XS/(sqrt(sqrt(S)^2 + sqrt(S)^2 + sqrt(S)^2 + sqrt(3XS)^2)). Where X is the multiplication factor applied to the no filter image so the R+G+B+L constructed luminance has the same S/N as eq.7 (i.e. the S/N of LRGB Luminance = to the S/N of the WCMY Luminance). Now if X=2 then:

9) The S/N of the LRGB luminance is S+S+S+6S/(sqrt(9S) = 9S/sqrt(9S) which is equal to the W luminance in equation 7.

So now we have a WCMY from 3 images and a LRGB from 4 images with equal Luminance and chrominance. The exposure time units for the LRGB was 1+1+1 and 2(the X component in equation 8) for the no filtered image and is equal to 5 time units.

The WCMY exposure time was (1+1+1) times 1.5 (the 50% increase in exposure time that was necessary to bring the S/N of the CMY derived RGBs up to the chrominance of S/N of the RGBs from RGB filters) = 4.5 time units.

The Bottom-Line (all things being equal which they rarely are!):

A WCMY with an equal S/N in both the chrominance and luminance to the S/N of a LRGB will require 3 images that are a total duration of 90% (4.5/5) as much as the total duration of the 4 images needed by the LRGB.

How does this work in real life? Below are two images, with equal exposure times, of the Globular Cluster M3.

M3 was imaged with equal exposures using CMY filters and RGB filters. The CMY image shows fainter stars and a greater expanse of the globular M3. Since each of the CMY color filters pass two colors of R, G, and B; the CMY image reaches to a fainter magnitude than the RGB image with equal exposures. Taken with a C14 @ f/7. The RGB is 5min. R, 10min. G, 15 min. B. The CMY image is 10min each C, M and Y.

............Ed Grafton

You are visitor number since a while back.